![[PukiWiki]](http://yoshio.velvet.jp/syswiki/image/life_jacket1.png "[PukiWiki]")
情報の基礎理論 †コンピュータを学習するうえで必要となる基礎事項・知識について解説します。 数値変換とデータ表現 †r進法 †10進法に代表されるr進法。 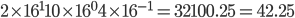 となります。 正の整数の表現 †2進数nけたで表現できる数 †２進数は各桁を0か1で表現します。２進数で表現できる正の数は 負数の表現 †2の補数 †一般的に負の数を表現する場合、補数というものが用いられます。 100000000 - 1 → N ---------- 011111111 → M N(１) + M(−１) = 0 このような考え方で２の負数を補数であらわします。 負数を表現する方法 †負数を表現する方法は３つあります。
小数点数の表現 †小数の表現 †一般的に小数だけで構成された数値を表現する場合は、最上位ビットの右側を小数点位置とします。これを固定小数点表現といいます。 01010000 = 0.625 |_小数点位置 11010000 = 0.625 - 1 = -0.375 |_小数点位置 小数点数の表現 †上記の固定小数点表現では整数部分を表現できません。そのため小数点を右に移動させ整数部分を拡張します。 01011010 = 5.625
|_小数点位置
11011010 = -2.375
|_小数点位置
浮動小数点数表現 †実数の表現 †7.25を有効桁数を表す仮数部と桁数を表す指数部に分けられる。 正規化 †浮動小数点表現で仮数部の最上位桁が0以外になるように桁を合わせることを正規化といいます。 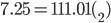 = 0 00000011 1110 1000 0000 0000 0000 000(浮動小数点4バイト) | | |_仮数部。ここが小数第１位 | |_指数部 |_正で0 有効けた数 †正規化した２進浮動小数点の有効桁数は仮数部の桁数で決まります。 アンダフローとオーバフロー †演算結果の絶対値が表現できる範囲を超えてしまった場合 → オーバーフロー 下回ってしまった場合 → アンダーフロー 誤差 †
集合と論理 †集合論理 †部分集合とべき集合 †集合とは、ある条件を満たし、ほかものとは明確に区別できるものの集まりをいいます。
|
は
です。
